二叉搜索树、红黑树 二叉搜索树(二叉排序树) 概念 二叉搜索树又称二叉排序树,具有以下性质:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树
注意:二叉搜索树中序遍历的结果是有序的。
基本操作 查找元素 思路: 二叉搜索树的左子树永远是比根节点小的,而它的右子树则都是比根节点大的值。当前节点比要找的大就往左走,当前元素比要找的小就往右走。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public Node search (int key) { if (root == null ){ return null ; } Node cur = root; while (cur != null ){ if (cur.val == key){ return cur; }else if (cur.val > key){ cur = cur.left; }else { cur = cur.right } } return null ; }
插入元素 如果是空树直接把元素插入root位置就好了。
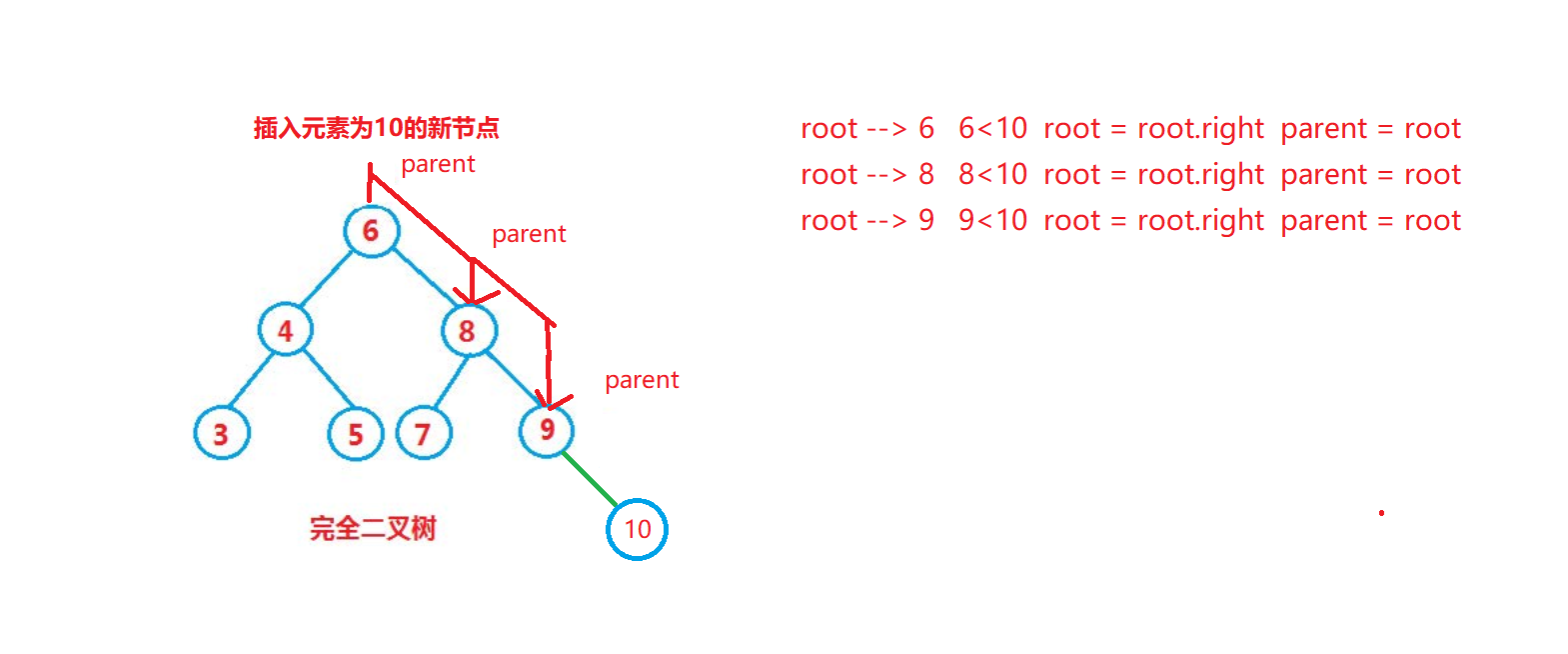
思路: 因为是二叉搜索树就不能插入重复的元素了,且每次插入都是插入到叶子节点的位置。定义一个 cur 从root开始,插入的元素比当前位置元素小就往左走,比当前位置元素大就往右走,直到为空,所以就需要再定义一个变量parent 记住 cur 的前面的位置。最后再判断插入到parent 的左子树还是右子树位置。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public boolean insert (int key) { Node node = new Node (key); if (root == null ){ this .root = node; return true ; } Node parent = null ; Node cur = root; while (cur != null ){ if (cur.val == key){ return false ; }else if (cur.val > key){ parent = cur; cur = cur.left; }else { parent = cur; cur = cur.right; } } if (parent.val > key){ parent.left = node; }else { parent.right = node; } return true ; }
删除元素 删除元素是一个比较难的点,要考虑到很多种情况
cur.left == null
cur是root,则root = cur.right
cur不是root,则cur是parent.left,则parent.left = cur.right
cur不是root,则cur是parent.right,则parent.right = cur.right
cur.right == null
cur是root,则root = cur.left
cur不是root,则cur是parent.left,则parent.left = cur.left
cur不是root,则cur是parent.right,则parent.right = cur.left
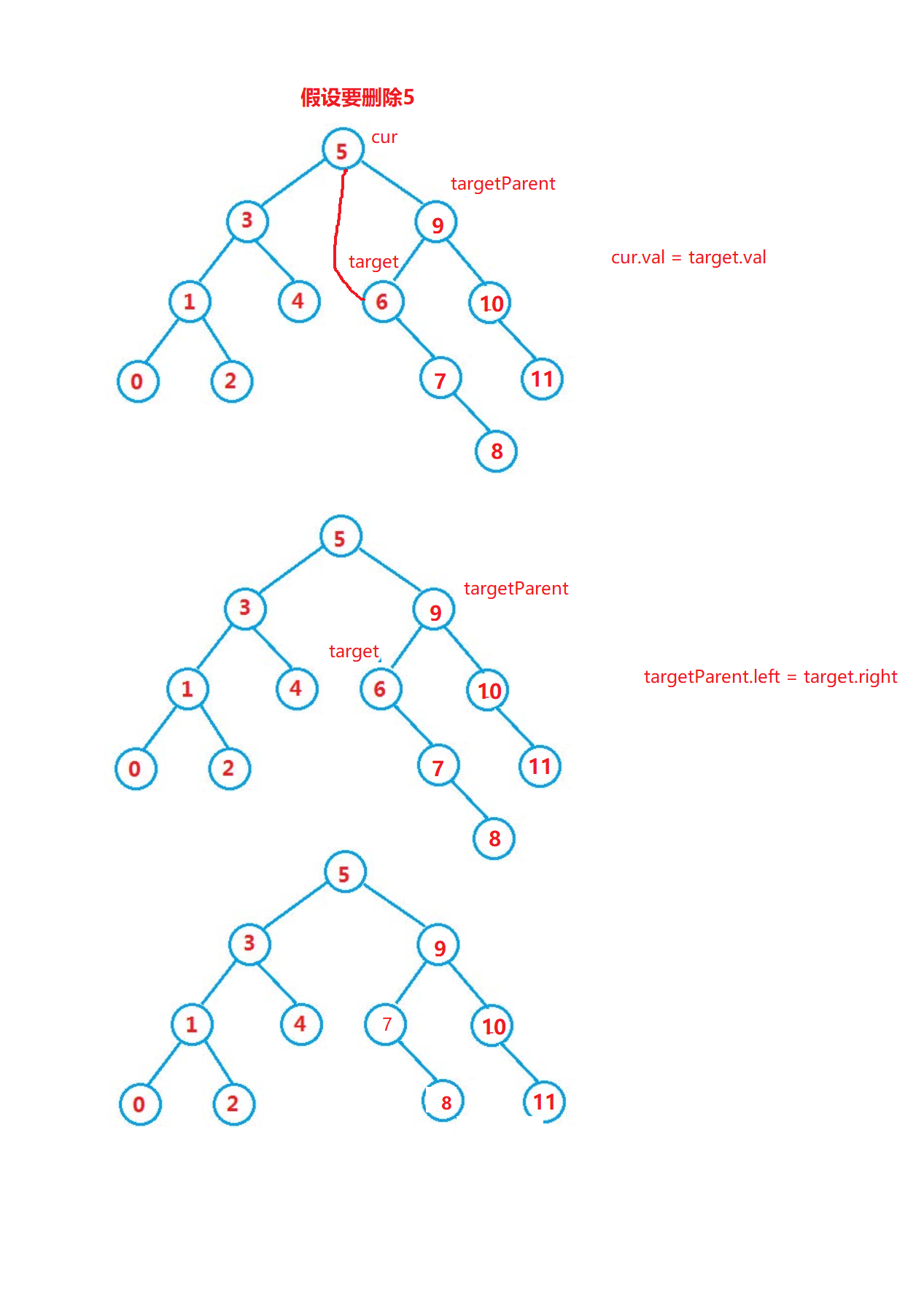
cur.left != null && cur.right != null
找到要删除节点,右树最左边的节点或者找到左树最右边的节点,替换这个两个节点的val值
这样才能保证,删除后左树一定比根节点小,右树一定比根节点大
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 public boolean remove (int key) { if (this .root == null ){ return false ; } Node parent = null ; Node cur = this .root; while (cur != null ){ if (cur.val == key){ removeKey(parent,cur); return true ; }else if (cur.val < key){ parent = cur; cur = cur.right; }else { parent = cur; cur = cur.left; } } return false ; } public void removeKey (Node parent,Node cur) { if (cur.left == null ){ if (this .root == cur){ this .root == this .root.left; }else if (cur == parent.left){ parent.left = cur.right; }else { parent.right = cur.right; } }else if (cur.right == null ){ if (this .root == cur){ this .root = this .root.left; }else if (cur == parent.left){ parent.left = cur.left; }else { parent.right = cur.left; } }else { Node targetParent = cur; Node target = cur.right; while (target.left != left){ targetParent = target; target = target.left; } cur.val = target.val; if (targetParent.left == target){ targetParent.left = target.right; }else { targetParent.right = target.right; } } }
性能分析 插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能
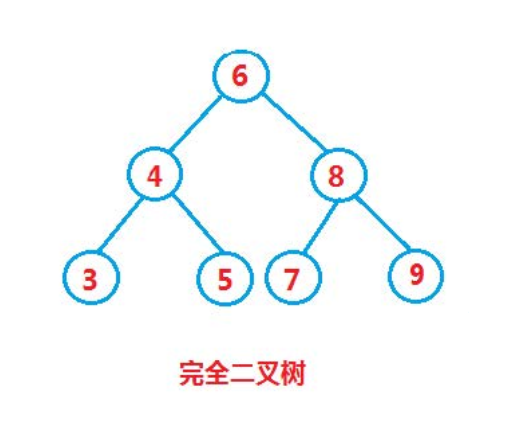
1 最好情况:二叉搜索树为完全二叉树,其平均比较次数为O(logn)
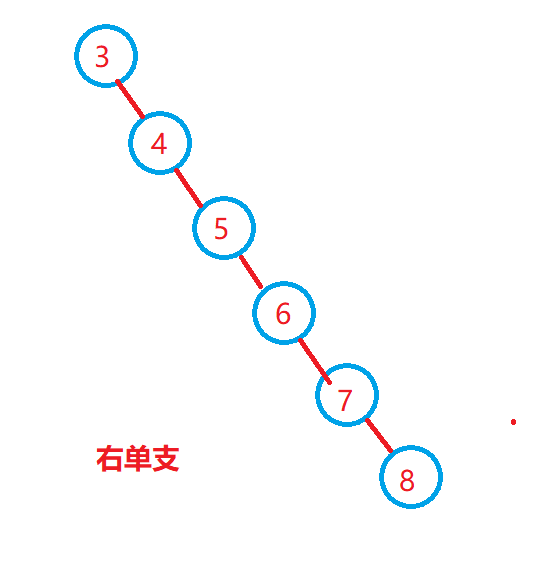
1 最坏情况:二叉搜索树退化为单支树,其平均比较次数为:O
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 public class BinarySearchTree { public static class Node { int val; Node left; Node right; public Node (int val) { this .val = val; } } public Node root = null ; public Node search (int key) { if (root == null ) { return null ; } Node cur = root; while (cur != null ) { if (cur.val == key) { return cur; }else if (cur.val > key) { cur = cur.left; }else { cur = cur.right; } } return null ; } public boolean insert (int key) { Node node = new Node (key); if (root == null ) { this .root = node; return true ; } Node parent = null ; Node cur = root; while (cur != null ) { if (cur.val == key) { return false ; }else if (cur.val > key) { parent = cur; cur = cur.left; }else { parent = cur; cur = cur.right; } } if (parent.val > key) { parent.left = node; }else { parent.right = node; } return true ; } public boolean remove (int key) { if (this .root == null ) { return false ; } Node parent = null ; Node cur = this .root; while (cur != null ) { if (cur.val == key) { removeKey(parent,cur); return true ; }else if (cur.val < key) { parent = cur; cur = cur.right; }else { parent = cur; cur = cur.left; } } return false ; } public void removeKey (Node parent,Node cur) { if (cur.left == null ) { if (cur == this .root) { this .root = this .root.right; }else if (cur == parent.left) { parent.left = cur.right; }else { parent.right = cur.right; } }else if (cur.right == null ) { if (this .root == cur) { this .root = this .root.left; }else if (cur == parent.left) { parent.left = cur.left; }else { parent.right = cur.left; } }else { Node targetParent = cur; Node target = cur.right; while (target.left != null ) { targetParent = target; target = target.left; } cur.val = target.val; if (targetParent.left == target) { targetParent.left = target.right; }else { targetParent.right = target.right; } } } }
红黑树原理 概述 红黑树的引入 有了二叉搜索树,为什么还需要平衡二叉树?
在学习二叉搜索树、平衡二叉树时,我们不止一次提到,二叉搜索树容易退化成一条链
这时,查找的时间复杂度从O(logN)也将退化成O(N)
引入对左右子树高度差有限制的平衡二叉树,保证查找操作的最坏时间复杂度也为O ( logN)
有了平衡二叉树,为什么还需要红黑树?
AVL的左右子树高度差不能超过1,每次进行插入/删除操作时,几乎都需要通过旋转操作保持平衡
在频繁进行插入/删除的场景中,频繁的旋转操作使得AVL的性能大打折扣
红黑树通过牺牲严格的平衡,换取插入/删除时少量的旋转操作,整体性能 优于AVL
红黑树插入时的不平衡,不超过两次旋转就可以解决;删除时的不平衡,不超过三次旋转就能解决
红黑树的红黑规则,保证最坏的情况下,也能在O(logN)时间内完成查找操作。
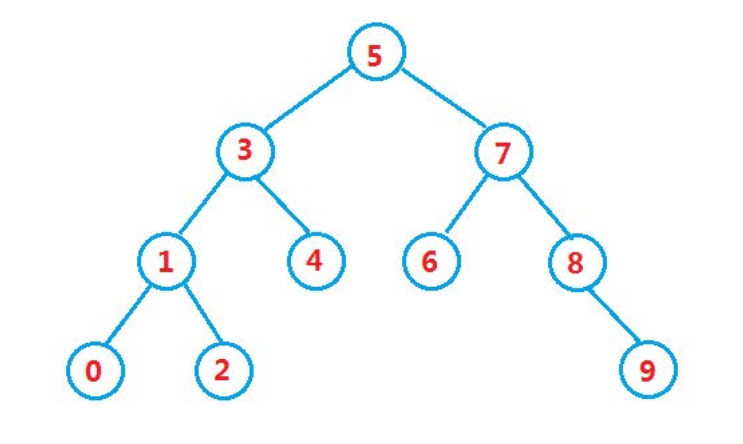
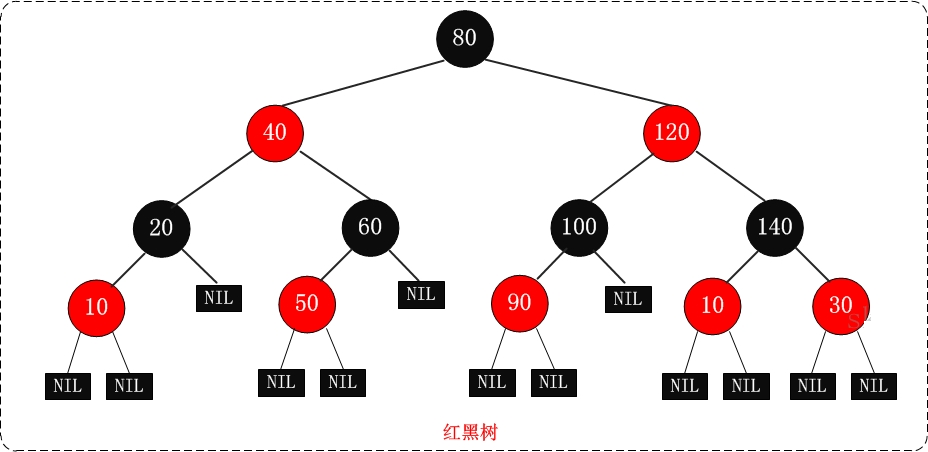
红黑规则 一棵典型的红黑树,如图所示
从图示,可以发现红黑树的一些规律:
节点不是红色就是黑色,根节点是黑色
红黑树的叶子节点并非传统的叶子节点,红黑树的叶子节点是null节点(空节点)且为黑色
同一路径,不存在连续的红色节点
红黑规则
节点不是黑色,就是红色(非黑即红)
根节点为黑色
叶节点为黑色(叶节点是指末梢的空节点 Nil或Null)
一个节点为红色,则其两个子节点必须是黑色的(根到叶子的所有路径,不可能存在两个连续的红色节点)
每个节点到叶子节点的所有路径,都包含相同数目的黑色节点(相同的黑色高度)
注意:
约束4和5,保证了红黑树的大致平衡 :根到叶子的所有路径中,最长路径不会超过最短路径的2倍。
使得红黑树在最坏的情况下,也能有O(logN)的查找效率
黑色高度为3时,最短路径:黑色→ 黑色 → 黑色,最长路径:黑色→ 红色 →黑色 → 红色 → 黑色
最短路径的长度为2(不算Nil的叶子节点),最长路径为4
关于叶子节点:Java实现中,null代表空节点,无法看到黑色的空节点,反而能看到传统的红色叶子节点
默认新插入的节点为红色:因为父节点为黑色的概率较大,插入新节点为红色,可以避免颜色冲突
红黑树的应用
Java中,TreeMap、TreeSet都使用红黑树作为底层数据结构
JDK 1.8开始,HashMap也引入了红黑树:当冲突的链表长度超过8时,自动转为红黑树
Linux底层的CFS进程调度算法中,vruntime使用红黑树进行存储。
多路复用技术的Epoll,其核心结构是红黑树 + 双向链表。
红黑树的左旋右旋 红黑树的定义
上一章节可知,红黑树要比二叉搜索树多一个颜色属性
同时,为了方便确认插入位置,还可以多一个parent属性,用于表示当前节点的父节点
因此,红黑树节点的定义如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 class RedBlackTreeNode { public int val; public RedBlackTreeNode left; public RedBlackTreeNode right; public boolean color; public RedBlackTreeNode parent; public RedBlackTreeNode () { } }
红黑树中,有一个root属性,用于记录当前红黑树的根节点
1 2 3 4 public class RedBlackTree { private RedBlackTreeNode root; }
红黑树的左旋 对于一棵红黑树,它满足红黑树的5条特性。插入或删除节点之后,红黑树就发生了变化,很可能不再完全满足红黑树的5条特性了,也就是不再是一棵红黑树了,而是一棵普通的二叉搜索树。这时候,为了使二叉搜索树重新变成红黑树,就需要对二叉搜索树进行操作,使它满足红黑树的5条特性。
以某个节点作为支点(旋转节点),其右子节点变为旋转节点的父节点,右子节点的左子节点变为旋转节点的右子节点,旋转节点的左子节点保持不变。右子节点的左子节点相当于从右子节点上“断开”,重新连接到旋转节点上。
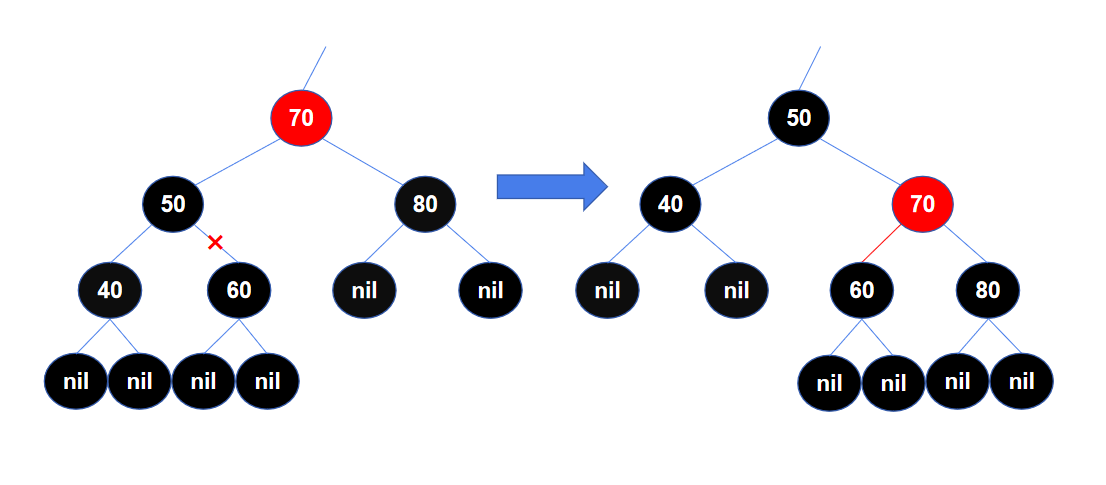
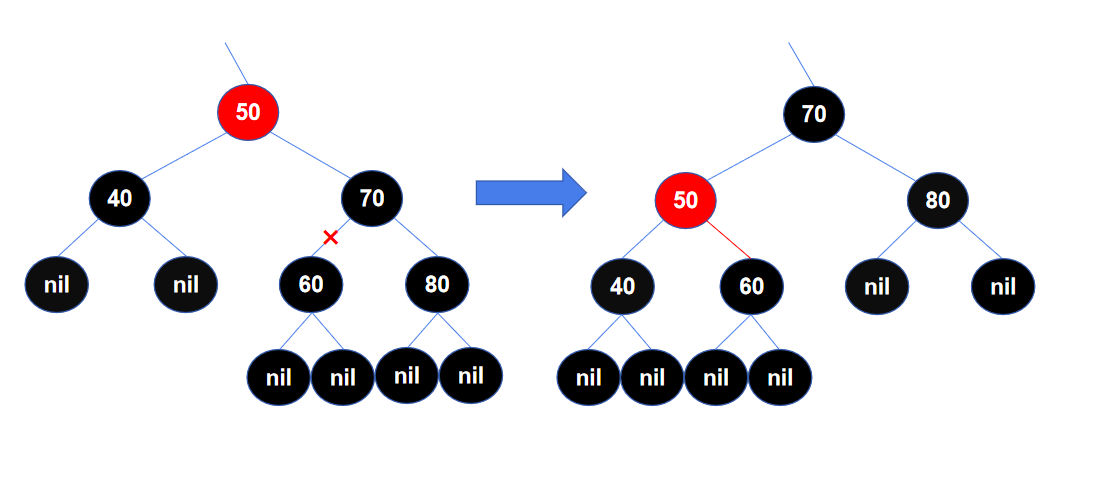
为了不失一般性,可以看下图中的例子。左边是左旋前的红黑树局部结构,先不考虑整体,只看局部,左旋前不满足红黑树的特性5。
左旋时,旋转节点为节点50,左旋后,旋转节点的右子节点70变为旋转节点50的父节点,右子节点的左子节点60从右子节点70上“断开”,成为旋转节点50的右子节点。
左旋后,结构如右图,这个局部重新满足了红黑树的特性5,达到目的。
具体实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 public void leftRotate (RedBlackTreeNode p) { if (p != null ) { RedBlackTreeNode rightChild = p.right; p.right = rightChild.left; if (rightChild.left != null ) { rightChild.left.parent = p; } rightChild.parent = p.parent; if (p.parent == null ) { this .root = rightChild; } else if (p == p.parent.left) { p.parent.left = rightChild; } else { p.parent.right = rightChild; } rightChild.left = p; p.parent = rightChild; } }
红黑树的右旋 以某个节点作为支点(旋转节点),其左子节点变为旋转节点的父节点,左子节点的右子节点变为旋转节点的左子节点,旋转节点的右子节点保持不变。左子节点的右子节点相当于从左子节点上“断开”,重新连接到旋转节点上。
不难看出,左旋和右旋是相反的,可逆的。
下图中的例子仍然是红黑树的局部,左边的结构不满足红黑树的特性5。
右旋时,旋转节点为节点70,右旋后,旋转节点的左子节点50变为旋转节点70的父节点,左子节点的右子节点60从左子节点50上“断开”,成为旋转节点70的左子节点。右旋后(右图),重新满足了红黑树的特性5。
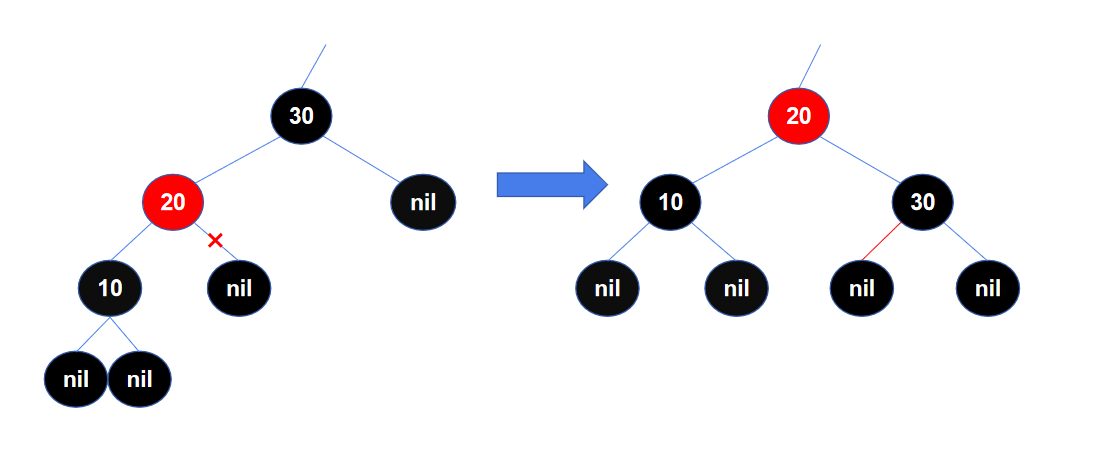
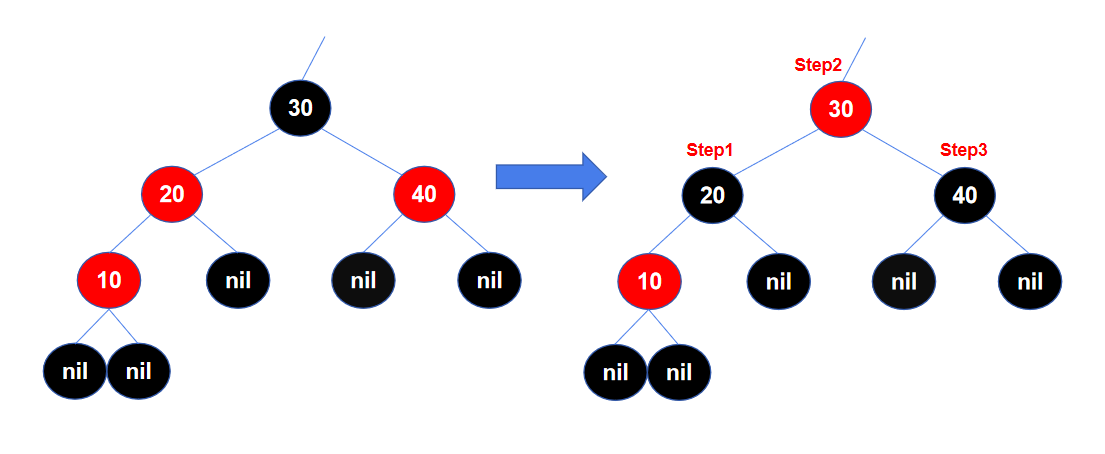
同样再看一个右旋的例子,左边是右旋前的局部结构,以节点30作为旋转节点,右旋后,旋转节点的左子节点20成为旋转节点30的父节点,左子节点的右子节点(这里是一个叶子节点NIL)从左子节点上“断开”,成为旋转节点30的左子节点。
具体实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public void rightRotate (RedBlackTreeNode p) { if (p != null ) { RedBlackTreeNode leftChild = p.left; p.left = leftChild.right; if (leftChild.right != null ) { leftChild.right.parent = p; } leftChild.parent = p.parent; if (p.parent == null ) { this .root = leftChild; } else if (p.parent.left == p) { p.parent.left = leftChild; } else { p.parent.right = leftChild; } leftChild.right = p; p.parent = leftChild; } }
红黑树的变色操作 当对红黑树进行插入或删除节点之后,如果不再完全满足红黑树的5条特性,除了旋转,变色也可以使二叉搜索树重新满足红黑树的5条特性。
变色:将节点的颜色由红变黑或由黑变红。
向红黑树中插入节点时,新节点的颜色都设置为红色。不管新节点是什么颜色,特性3都不可能被破坏,特性1、2、4都有可能被破坏。如果插入的节点是黑色,则一定会破坏特性5,需要进行调整,如果插入的节点是红色,则一定不会破坏特性5。所以将新节点设置为红色,可以降低破坏红黑树特性的可能性。
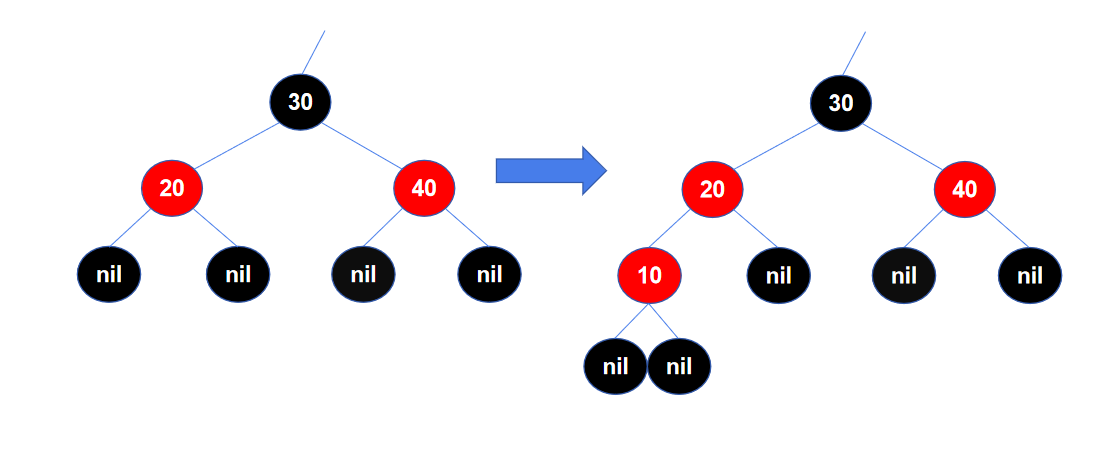
添加节点 如下的左图是红黑树的一个局部,一开始是满足红黑树的特性的,在其中插入了红色节点10,两个红节点连在一起了,不再满足红黑树的特性4。
通过变色,先将节点20变成黑色,特性4满足了,但又不满足特性5,所以继续将节点30变成红色,节点40变成黑色。
经过3次变色后,从局部看,已经重新满足了红黑树的特性。但是,从整棵树来看,还不一定满足红黑树的特性,如果节点30的父节点也是红色,则还需要继续对这棵树进行调整(上面的左旋和右旋例子中也有这种情况)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 public void fixAfterInsert (RedBlackTreeNode x) { x.color = RED; while (x != null && this .root != x && x.parent.color == RED) { if (parentOf(x) == parentOf(parentOf(x)).left) { RedBlackTreeNode uncle = parentOf(parentOf(x)).right; if (uncle.color == RED) { parentOf(x).color = BLACK; uncle.color = BLACK; parentOf(parentOf(x)).color = RED; x = parentOf(parentOf(x)); } else { if (x == parentOf(x).right) { x = parentOf(x); leftRotate(x); } parentOf(x).color = BLACK; parentOf(parentOf(x)).color = RED; rightRotate(parentOf(parentOf(x))); } } else { RedBlackTreeNode uncle = parentOf(parentOf(x)).left; if (uncle.color == RED) { parentOf(x).color = BLACK; uncle.color = BLACK; parentOf(parentOf(x)).color = RED; x = parentOf(parentOf(x)); } else { if (parentOf(x).left == x) { x = parentOf(x); rightRotate(x); } parentOf(x).color = BLACK; parentOf(parentOf(x)).color = RED; leftRotate(parentOf(parentOf(x))); } } } this .root.color = BLACK; } private static RedBlackTreeNode parentOf (RedBlackTreeNode p) { return (p == null ? null : p.parent); }
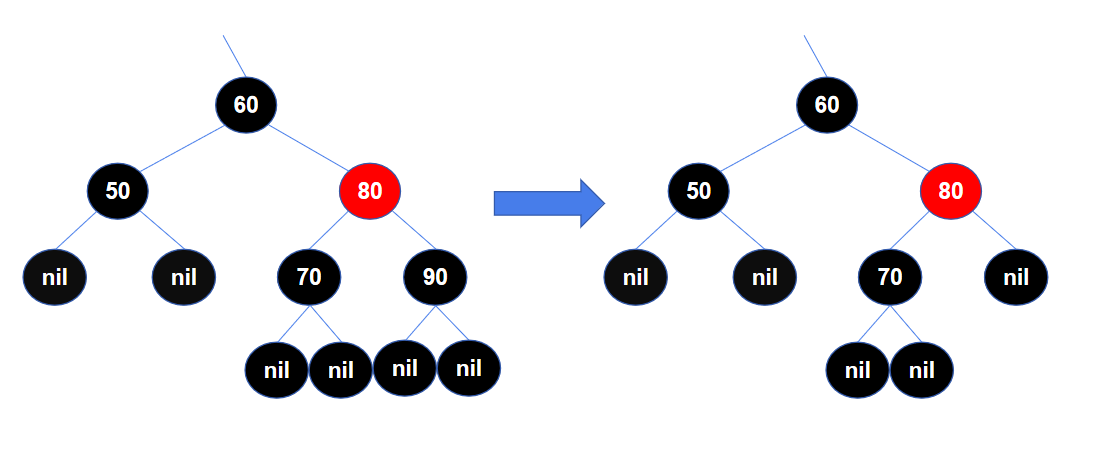
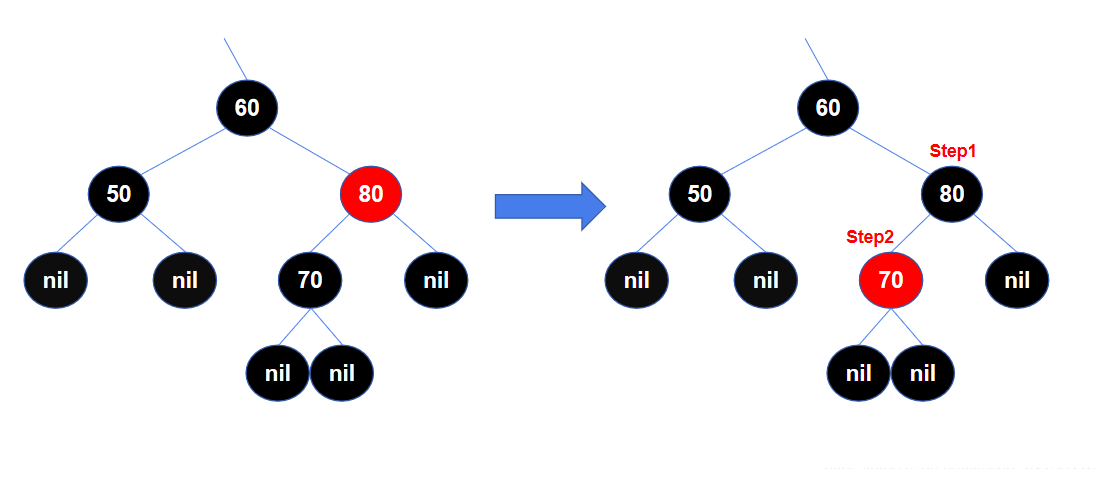
删除节点 如下的左图是红黑树的一个局部,一开始是满足红黑树的特性的,将节点90删除后,不再满足红黑树的特性5。
通过变色,先将节点80变成黑色,但仍不满足特性5,继续将节点70变成红色,重新满足了红黑树的特性。
经过两次变色,重新满足了红黑树的特性,对于这个例子,只要局部满足了,整棵树一定是满足红黑树的。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 public void fixAfterDeletion (RedBlackTreeNode x) { while (x != root && x.color == BLACK) { if (x == parentOf(x).left) { RedBlackTreeNode brother = parentOf(x).right; if (brother.color == RED) { brother.color = BLACK; parentOf(x).color = RED; leftRotate(parentOf(x)); brother = parentOf(x).right; } if (brother.left.color == BLACK && brother.right.color == BLACK) { brother.color = RED; x = parentOf(x); } else { if (brother.right.color == BLACK) { brother.left.color = BLACK; brother.color = RED; rightRotate(brother); brother = parentOf(x).right; } brother.color = parentOf(x).color; parentOf(x).color = BLACK; brother.right.color = BLACK; leftRotate(parentOf(x)); x = root; } } else { RedBlackTreeNode brother = parentOf(x).left; if (brother.color == RED) { brother.color = BLACK; parentOf(x).color = RED; rightRotate(parentOf(x)); brother = parentOf(x).left; } if (brother.left.color == BLACK && brother.right.color == BLACK) { brother.color = RED; x = parentOf(x); } else { if (brother.left.color == BLACK) { brother.right.color = BLACK; brother.color = RED; leftRotate(brother); brother = parentOf(x).left; } brother.color = parentOf(x).color; brother.left.color = BLACK; parentOf(x).color = BLACK; rightRotate(parentOf(x)); x = root; } } } x.color = BLACK; }
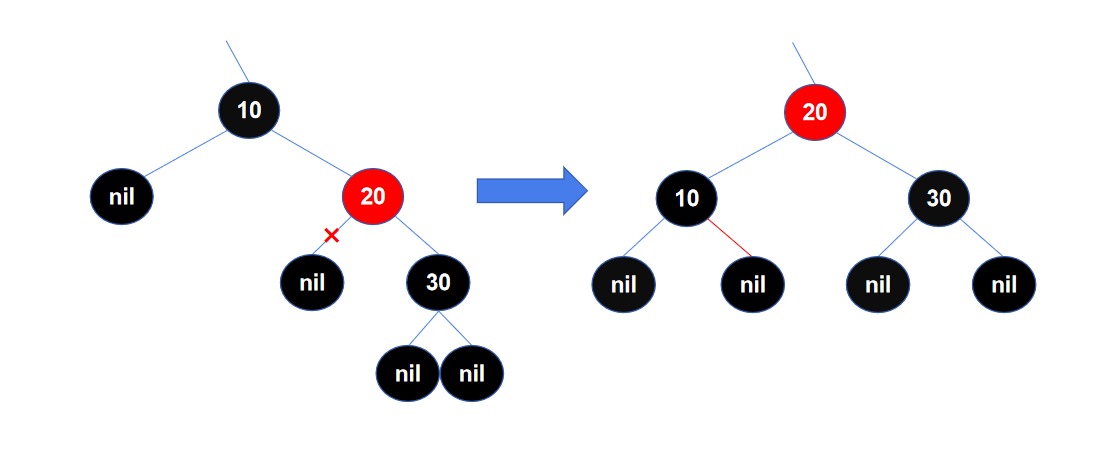
 再看另一个左旋的例子,左边是左旋前的局部结构,以节点10作为旋转节点,左旋后,旋转节点的右子节点20成为旋转节点10的父节点,右子节点的左子节点(这里是一个叶子节点NIL)从右子节点上“断开”,成为旋转节点10的右子节点。
再看另一个左旋的例子,左边是左旋前的局部结构,以节点10作为旋转节点,左旋后,旋转节点的右子节点20成为旋转节点10的父节点,右子节点的左子节点(这里是一个叶子节点NIL)从右子节点上“断开”,成为旋转节点10的右子节点。